Новый математический аппарат
Из проведенных исследований видно, что граф алгоритма и развертки являются теми объектами, которые могут стать основой создания математического аппарата, предназначенного для изучения информационной структуры алгоритмов. Но чтобы эти объекты превратились в действенные инструменты, они должны быть представлены в форме, удобной для проведения как теоретических исследований, так и практических расчетов. При выборе формы необходимо учитывать, что в реальности все операции с графом алгоритма и развертками в силу их сложности придется выполнять на компьютере. Принимая во внимание необходимость обеспечения широкой доступности процессов изучения структуры алгоритмов, этот компьютер, скорее всего, должен быть персональным. Поэтому выбор форм представления графов алгоритмов и разверток должен учитывать и эффективность предстоящей работы с ними.
В теоретическом отношении вроде бы все устроено достаточно хорошо. Представление графа алгоритма ориентированным ациклическим графом, а разверток вещественными функционалами оказалось эффективным. Кажется, что использование линейных функционалов в качестве разверток открывает неплохие практические перспективы. Однако все предположения, которые до сих пор были сделаны относительно графа алгоритма, к реальной практике имеют весьма слабое отношение.
Одно из первых теоретических предположений связано с размещением графа в некотором арифметическом пространстве подходящей размерности. Такое предположение существенно, так как с помощью достаточно простых средств позволяет обеспечить возможность построения разверток, выполнение операций над ними, введение линейных разверток через скалярное произведение и т.д. Но как конструктивно строить это пространство, какова его размерность и как именно в нем должны быть расположены вершины? Ведь уже на примере регулярных графов было отмечено, что допущение излишней свободы в размещении вершин может привести к потере важных структурных свойств. И вообще, откуда брать информацию о графе алгоритма? Он же почти никогда не бывает известен ни в теории, ни тем более на практике! В реальных алгоритмах число вершин графа настолько велико, что становится ясно: не может даже идти речь ни о каком описании графов, основанном на прямом перечислении всех его вершин и дуг. Но тогда как же его описывать и как исследовать?
Ответы на все эти вопросы надо искать на пути анализа используемых форм записи алгоритмов. Других источников, из которых можно было бы получить информацию о графах алгоритмов, просто не существует. Заметим, что для описания алгоритмов массово используются только две формы - это записи в виде различных математических соотношений и программы на алгоритмических языках. У каждой из форм имеются как достоинства, так и недостатки. Основное достоинство программ заключается в том, что с их помощью можно дать точное описание алгоритма без каких-либо недомолвок и неоднозначностей. Однако их очень трудно анализировать, главным образом, из-за пересчета содержимого ячеек памяти. В математических записях нет пересчета памяти, и в этом заключается их большое преимущество перед программами. Но обычно в них остаются различные недомолвки и неоднозначности, особенно в отношении порядка выполнения операций. Поэтому для точного изложения содержания математических записей все равно приходится пользоваться какими-то алгоритмическими языками. Наиболее приемлемыми для выявления сведений о графе алгоритма могли бы быть программы на языках однократного присваивания, поскольку в них нет пересчета памяти, но сам алгоритм описывается точно. К сожалению, багаж алгоритмов, записанных на таких языках, очень скуден.
Принимая во внимание высказанные соображения, остановимся на языке типа фортран в качестве формы описания алгоритмов. Аргументов в пользу выбора данного языка несколько. Во-первых, он наиболее близок к математическому описанию алгоритмов. Во-вторых, в вычислительной математике этот язык всегда был и остается до сих пор самым используемым языком программирования. И, наконец, на нем накоплен самый большой в мире багаж алгоритмов. Иметь возможность использовать такой багаж для выявления структуры алгоритмов в вычислительной математике - заманчивая перспектива.
Не все конструкции языка фортран будут использоваться в одинаковой мере. Для начала исследований выделим относительно простой, но достаточно содержательный класс программ. На нем попытаемся понять основные особенности устройства графов алгоритмов. И только после этого приступим к расширению выбранного класса. Будем считать сейчас, что алгоритм записан с помощью следующих средств языка:
- в программе может использоваться любое число простых переменных и переменных с индексами;
- единственным типом исполнительного оператора может быть оператор присваивания, правая часть которого есть арифметическое выражение; допускается любое число таких операторов;
- все повторяющиеся операции описываются только с помощью циклов
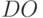 ; структура вложенности циклов может быть произвольной; шаги изменения параметров циклов всегда равны +1; если у цикла нижняя граница больше верхней, то цикл не выполняется;
; структура вложенности циклов может быть произвольной; шаги изменения параметров циклов всегда равны +1; если у цикла нижняя граница больше верхней, то цикл не выполняется; - допускается использование любого числа условных и безусловных операторов перехода "вниз" по тексту; не допускается использование побочных выходов из циклов;
- все индексные выражения переменных, границы изменения параметров циклов и условия передач управления заданы явно; они являются линейными функциями как по параметрам циклов, так и по внешним переменным программы; коэффициенты всех линейных функций являются целыми числами;
- внешние переменные программы (размеры массивов и т.п.) всегда целочисленные, и вектора их значений принадлежат некоторым целочисленным многогранникам;
- в целях наглядности описания программы, а также для организации управления вычислительным процессом все или часть операторов могут быть помечены.
Программы, удовлетворяющие описанным условиям, будем называть линейными или принадлежащими линейному классу. Они и будут предметом ближайших исследований. Обратим внимание на одно очень важное обстоятельство, вызывающее, к тому же, немалые трудности при проведении этих исследований. Именно, все возникающие задачи придется решать в условиях, когда конкретные значения внешних переменных известны только перед началом работы программы и неизвестны в момент ее исследования. Поэтому все задачи неизбежно окажутся задачами с неизвестными параметрами.
Особая специфика записи операторов не потребуется. Если нужно приблизить форму записи алгоритмов к математической, то будем писать индексы переменных так же, как в математических соотношениях, т.е. справа от переменных снизу и/или сверху. Сделаем также некоторое уточнение, касающееся переменной с индексами. Обычно под этим понятием рассматривается весь массив простых переменных, объединенных общим идентификатором. При изучении тонкой структуры программы гораздо удобнее рассматривать массив как группу простых переменных, идентификаторы которых составлены из идентификатора массива и индексов. Всюду в дальнейшем будем понимать под переменной с индексами отдельный элемент массива.
Как показывает статистика, многие значимые фрагменты практически используемых программ непосредственно принадлежат линейному классу. Еще большее число фрагментов сводится к нему. Линейный класс играет такую же роль в изучении структуры программ как линейные функции в математическом анализе, линейные неравенства в задачах оптимизации, линейная алгебра в вычислительной математике и т.п.
Важнейшая цель ближайших исследований состоит в нахождении графа алгоритма, описанного программой из линейного класса. Подчеркнем, что достижение цели планируется обеспечить исключительно на основе анализа текста программ без привлечения какой-либо дополнительной информации. В силу большого объема выкладок мы не будем проводить сейчас детальные исследования, а ограничимся описанием лишь их общей схемы. Все необходимые подробности можно найти в [ 1 ] .
Прежде всего нужно точно описать множество вершин графа алгоритма.
Пусть задана произвольная линейная программа. Перенумеруем подряд
сверху вниз все операторы присваивания и обозначим их через  .
С каждым оператором присваивания
.
С каждым оператором присваивания  , свяжем тесно вложенное гнездо
циклов. Оно получается путем оставления в программе только тех циклов
, свяжем тесно вложенное гнездо
циклов. Оно получается путем оставления в программе только тех циклов 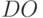 , в тела которых входит рассматриваемый оператор. Рассмотрим
арифметическое пространство, координаты которого определяются
параметрами данного гнезда. Назовем это пространство опорным для
оператора
, в тела которых входит рассматриваемый оператор. Рассмотрим
арифметическое пространство, координаты которого определяются
параметрами данного гнезда. Назовем это пространство опорным для
оператора  и будем считать, что в нем естественным образом введены
линейные операции и скалярное произведение. Границы изменения
параметров определяют в опорном пространстве линейный многогранник,
который будем также называть опорным и обозначать
и будем считать, что в нем естественным образом введены
линейные операции и скалярное произведение. Границы изменения
параметров определяют в опорном пространстве линейный многогранник,
который будем также называть опорным и обозначать 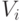 . Его границы
зависят от внешних переменных. Поэтому в общем случае от них будут
зависеть размеры всех опорных многогранников и их конфигурации. Как
правило, с ростом значений внешних переменных размеры многогранников
неограниченно увеличиваются. Напомним, что значения внешних переменных
на момент проведения исследований не известны.
. Его границы
зависят от внешних переменных. Поэтому в общем случае от них будут
зависеть размеры всех опорных многогранников и их конфигурации. Как
правило, с ростом значений внешних переменных размеры многогранников
неограниченно увеличиваются. Напомним, что значения внешних переменных
на момент проведения исследований не известны.
Каждая операция алгоритма однозначно определяется номером  соответствующего оператора
соответствующего оператора  и значениями параметров относящегося к
нему гнезда циклов. Исторически принято отдельное срабатывание
оператора
и значениями параметров относящегося к
нему гнезда циклов. Исторически принято отдельное срабатывание
оператора  называть итерацией. Поэтому совокупность опорных областей
называть итерацией. Поэтому совокупность опорных областей 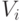 для
для  будем называть пространством итераций. Оно
состоит из линейных многогранников, принадлежащих разным
арифметическим пространствам, имеющим, чаще всего, разные размерности.
Факт, что некоторые или даже все многогранники могут порождаться
одними и теми же значениями параметров циклов, не имеет сейчас
никакого значения. Это будет отражаться лишь в том, что такие
многогранники будут в чем-то похожи по расположению в своих
пространствах и иметь какие-то размеры одинаковыми. В пространстве
итераций положение всех вершин графа алгоритма определено однозначно.
Конечно, построенное пространство не является арифметическим, как это
предполагалось ранее. Однако ничто не мешает при необходимости
расширить пространство итераций до арифметического пространства,
считать вершины графа векторами, ввести линейные операции над ними и
т.д.
будем называть пространством итераций. Оно
состоит из линейных многогранников, принадлежащих разным
арифметическим пространствам, имеющим, чаще всего, разные размерности.
Факт, что некоторые или даже все многогранники могут порождаться
одними и теми же значениями параметров циклов, не имеет сейчас
никакого значения. Это будет отражаться лишь в том, что такие
многогранники будут в чем-то похожи по расположению в своих
пространствах и иметь какие-то размеры одинаковыми. В пространстве
итераций положение всех вершин графа алгоритма определено однозначно.
Конечно, построенное пространство не является арифметическим, как это
предполагалось ранее. Однако ничто не мешает при необходимости
расширить пространство итераций до арифметического пространства,
считать вершины графа векторами, ввести линейные операции над ними и
т.д.
Значительно сложнее подобраться к пониманию того, в какой форме должны описываться дуги. Представление графа алгоритма произвольным ориентированным ациклическим графом не подсказывает никакой идеи о формах их описания в реальных алгоритмах. Может даже создаться впечатление, что допустимым является любое расположение дуг вплоть до хаотического. Как будто бы близкое к этому расположение даже реализуется на алгоритмах, связанных с нерегулярными и адаптивными сетками. С другой стороны, большого хаоса вроде бы не должно быть. Дуги графа алгоритма отражают информационные отношения между отдельными операциями. Эти же отношения, но только в скрытом виде, присутствуют и в математических записях, и в программах. Принимая во внимание огромный объем вычислений в реальных задачах, хаотические информационные отношения между отдельными операциями могут описываться только через очень длинные записи и программы. Однако на практике и математические записи и программы, как правило, достаточно компактны. Поэтому, скорее всего, дуги графов реальных алгоритмов должны описываться как-то иначе и проще. Например, с помощью каких-то не слишком сложных функций. Начнем исследование возможных форм представления дуг с линейного класса программ.
Количество входных переменных в каждом операторе конечно. Поэтому
формально граф алгоритма можно описать некоторой конечнозначной
функцией  . Для любой точки
. Для любой точки  пространства итераций множество значений
функции
пространства итераций множество значений
функции  есть множество тех точек того же пространства, из которых
идут дуги графа в точку
есть множество тех точек того же пространства, из которых
идут дуги графа в точку  . В общем случае число значений функции
. В общем случае число значений функции  может быть различным в разных точках. Более того, разные значения
функции
может быть различным в разных точках. Более того, разные значения
функции  в одной точке
в одной точке  могут принадлежать разным опорным
многогранникам. Всегда существуют точки, в которых функция
могут принадлежать разным опорным
многогранникам. Всегда существуют точки, в которых функция  не
определена. К ним относятся точки, соответствующие операциям, где в
качестве аргументов используются лишь входные данные. Принципиальный
вопрос состоит в выяснении того, как устроена функция
не
определена. К ним относятся точки, соответствующие операциям, где в
качестве аргументов используются лишь входные данные. Принципиальный
вопрос состоит в выяснении того, как устроена функция  .
.
Пусть в пространстве итераций задана система однозначных функций  . Предположим, что область определения каждой из них принадлежит
какому-то одному опорному многограннику, а область значений - тому же
или другому многограннику. Допустим, что для каждой точки
. Предположим, что область определения каждой из них принадлежит
какому-то одному опорному многограннику, а область значений - тому же
или другому многограннику. Допустим, что для каждой точки  пространства итераций при любых значениях внешних переменных найдется
среди функций
пространства итераций при любых значениях внешних переменных найдется
среди функций  такая подсистема, что множество значений функции
такая подсистема, что множество значений функции  совпадает со значениями в точке
совпадает со значениями в точке  функций из данной подсистемы. Будем
говорить, что в этом случае граф покрывается системой функций
функций из данной подсистемы. Будем
говорить, что в этом случае граф покрывается системой функций  , а
сами функции
, а
сами функции  будем называть покрывающими. Для всех исследований,
проводимых с графом алгоритма, фундаментальное значение имеет
[
1
]
будем называть покрывающими. Для всех исследований,
проводимых с графом алгоритма, фундаментальное значение имеет
[
1
]
