НОУ ИНТУИТ | Введение в схемы, автоматы и алгоритмы. Лекция 10: Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Тверской государственный университет

Опубликован: 21.08.2007 | Доступ: свободный | Студентов: 1684 / 243 | Оценка: 5.00 / 5.00 | Длительность: 14:18:00

ISBN: 978-5-94774-714-0

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема 10.5. Все проблемы, перечисленные выше в пунктах 1-4, являются алгоритмически неразрешимыми.

Доказательство. Нам потребуются следующие вспомогательные программы 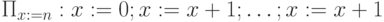$\Pi _{x:=n}: x:=0; x:= x+1; \dots ; x:= x+1$ ( присваиваие x:=x+1 повторяется n раз). Понятно, что для любого начального состояния $\sigma$ после выполнения $\Pi _{x:=n}$ имеем $\Pi _{x:=n}(\sigma )(x)=n$ .

Докажем неразрешимость {проблемы останова:} по произвольной структурированной программе $\Pi$ определить, завершится ли вычисление $\Pi$ на входе 0. Пусть $M_{h0}=\{ n | \Phi _{\Pi n,y }(0) < \infty \}$ . Докажем, что множество номеров самоприменимых программ M_s сводится к M_h0. Пусть n - номер программы $\Pi _{n}$ . преобразуем ее в программу $\Pi ': \Pi _{x:=n};\Pi _{n}; y:=0$ . Таким образом, $\Pi '$ вначале заносит в x номер n программы $\Pi _{n}$ , а затем применяет $\Pi _{n}$ к этому номеру и, если $\Pi _{n}$ на n останавливается, выдает результат y=0. Поэтому $\Pi '$ останавливается на любом аргументе (в том числе и на 0) тогда и только тогда, когда $n \in M_{s}$ . Преобразование программы $\Pi _{n}$ в программу $\Pi '$ осуществляется эффективно. Поэтому (на основании тезиса Тьюринга-Черча) существует такая о.р.ф. f, которая по n вычисляет номер m программы $\Pi '=\Pi _{m}=\Pi _{f(n)}$ . Эта функция и будет сводить M_s к M_h0, так как $n \in M_{s} \Leftrightarrow f(n) \in M_{h0}$ . Следовательно, по лемме ref{lm-red} проблемы останова M_h0 неразрешима.

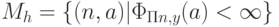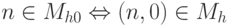Очевидно, что и более общая форма проблемы останова $M_{h}=\{ (n,a) | \Phi _{\Pi n, y }(a) < \infty \}$ также неразрешима, поскольку к ней сводится M_h0: $n \in M_{h0} \Leftrightarrow (n,0) \in M_{h}$ .
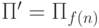Для сведения M_s к множеству M_t номеров программ, вычисляющих всюду определенные функции, можно также использовать функцию f из пункта 1. Действительно, $\Pi _{n}$ останавливается на входе n тогда и только тогда, когда $\Pi '=\Pi _{f(n)}$ останавливается на всех входах, т.е. $n\in M_{s} \Leftrightarrow f(n) \in M_{t}$ . Следовательно, проблема тотальности M_t неразрешима.
Рассмотрим теперь проблему эквивалентности. Пусть

$M_{eq}=\{(n,m) | \textit{ для всех } x \\ \Phi_{\Pi_n,y}(x) = \Phi_{\Pi_m,y}(x) \}.$ ( x) )

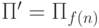Зафиксируем следующую программу P⁰: x:=x; y:=0. Очевидно, что она вычисляет функцию, тождественно равную нулю, т.е. $\Phi_{P^0,y}(x)=0$ для всякого x. Пусть ее номер n(P⁰) равен k₀. Для произвольного n рассмотрим пару (f(n), k₀). Из определения f следует, что $\Pi _{n}$ останавливается на входе n тогда и только тогда, когда $\Pi '=\Pi _{f(n)}$ останавливается на всех входах и выдает результат 0: $\Phi_{\Pi_{f(n),y}}(x)=0$ для всех x, т.е. $\Pi _{ f(n)}$ и $\Pi_{k_0}$ эквивалентны. Тогда $n \in M_{s}\Leftrightarrow (f(n),k_{0}) \in M_{eq}$ . Положим g(n)= c₂(f(n),k₀) . Тогда g является о.р.ф. 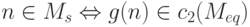и $n \in M_{s}\Leftrightarrow g(n) \in c_{2}(M_{eq})$ . Следовательно, M_s сводится к M_eq посредством g и проблема M_eq неразрешима.
Для доказательства неразрешимости проблемы лишнего присваивания:

$M_{opt1}=\{(n,m) | \textit{на некотором входе } \ a\ \textit{ в программе } \ \Pi_n \textit{срабатывает }\\ m\textit{-ый по счету } \textit{оператор присваивания}\}$

снова используем функцию f из пункта 1. Напомним, что $\Pi _{f(n)}: \Pi _{\{ }x:=n\} ;\Pi _{n}; y:=0$ . По n и соответствующей программе $\Pi _{n}$ можно легко определить номер m последнего присваивания y:=0 в $\Pi _{f(n)}$ :

$m= (n+1) + (\textit{число присваиваний в } \Pi_n) +1$

Пусть g(n) - это о.р.ф., вычисляющая по n этот номер m. Тогда $n \in M_{s}\Leftrightarrow (f(n),g(n)) \in M_{opt1}$ . Положим h(n)= c₂(f(n),g(n)). Тогда h является о.р.ф. и $n \in M_{s}\Leftrightarrow h(n) \in c_{2}(M_{opt1})$ . Следовательно, M_s сводится к M_opt1 посредством h и проблема M_opt1 неразрешима.

Рассмотрим теперь проблему лишнего условия:

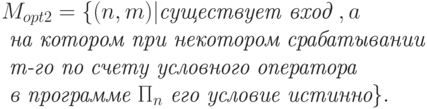
$M_{opt2}=\{(n,m) | \textit{существует вход\ }, a\\ \textit{ на котором при некотором срабатывании}\\\textit{ m-го по счету условного оператора}\\\textit{ в программе } \Pi_n\ \textit{его условие истинно}\}.$

Для доказательства ее неразрешимости определим по n программу $\Pi ’‘: \Pi ’; если y=0 то y:=y иначе y:=y +1 конец$ ( здесь $\Pi '$ - программа из п. 1). И в этом случае программа $\Pi ''$ строится по программе $\Pi _{n}$ эффективно. Пусть ее номер вычисляется о.р.ф. f’, т.е. $\Pi _{f’(n)}=\Pi ''$ , и пусть о.р.ф. g’(n) определяет номер последнего условного оператора в программе $\Pi _{f’(n)}$ . Тогда $n \in M_{s}\Leftrightarrow$ в программе $\Pi _{f'(n)}$ последний условный оператор выполняется (на любом входе) и при этом y=0, т.е. его условие истинно, а это означает, что $(f’(n),g'(n)) \in M_{opt2}$ . 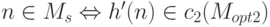Положив h’(n)= c₂(f’(n),g’(n)), получим, что $n \in M_{s} \Leftrightarrow h'(n) \in c_{2}(M_{opt2})$ . Следовательно, M_s сводится к M_opt2 посредством h’ и проблема M_opt2 также неразрешима.

Теорема доказана.

Какой же вывод можно сделать из того, что некоторая алгоритмическая проблема оказалась неразрешимой? Для программистов из такого утверждения извлекаются "две новости: плохая и хорошая ". "Плохая новость" состоит в том, что невозможно построить алгоритм (программу) для автоматического решения такой проблемы. Например, из теоремы 10.5 следует, что невозможно автоматически проверить, входит ли некоторый вход в область определения вычислимой функции, нельзя определить корректность программы, т.е. то, что она вычисляет требуемую функцию, нет способа проверять эквивалентность программ (не только структурированных, но и написанных на Паскале, Си, ассемблере, Яве и других языках программирования), не существует алгоритмов для оптимизаций, связанных с удалением лишних присваиваний и условий, и т.п. Но неразрешимость проблемы не означает, что она не может быть решена для некоторых отдельных входных данных. Например, в предыдущих разделах мы построили достаточно много программ и доказали их корректность. Поэтому "хорошая новость" для программистов и математиков состоит в том, что их труд при решении неразрешимых проблем в каждом отдельном случае является творческим - никакой программой их не заменить. Появление каждой новой содержательно интересной неразрешимой проблемы только расширяет область их творчества, заставляет искать все более и более широкие алгоритмы, которые позволяют решать все более обширные подклассы относящихся к этой проблеме индивидуальных задач.

Задачи

Задача 10.1. Докажите, что машины Тьюринга $\mathcal{ M}_F$ и $\mathcal{M}_f$ , определенные в доказательстве теоремы 10.1 для примитивной рекурсии и минимизации, действительно правильно реализуют указанные операторы.

Задача 10.2. Постройте машины Тьюринга Mⁱ₀ , Mⁱ₊₁, M^ij, $\Phi ^{ ij }_{=}$ , $\Phi ^{ ij}_{<}$ , M_start и M_end, определенные в доказательстве теоремы 10.2.

Задача 10.3. Докажите утверждение 1, сформулированное в доказательстве теоремы 10.2, используя индукцию по построению программы $\Pi$ и соответствующей м.Т. $M_{\Pi }$ .

Задача 10.4. В доказательстве теоремы 10.3 рассмотрен случай, когда м.Т. $\mathcal{ M}$ вычисляет функцию от одного аргумента f(x) . Покажите, что теорема верна и в общем случае для функций f(x₁,...,x_n) при любом n.

Задача 10.5. Докажите, что отношение алгоритмической сводимости <=_m является рефлексивным и транзитивным.

Задача 10.6. Доказать алгоритмическую неразрешимость следующих проблем.

По произвольной программе $\Pi$ определить, является ли вычисляемая ей функция $\Phi _{\Pi ,y}(x)$ постоянной константой.
По произвольной программе $\Pi$ и числам a и b проверить равенство $\Phi _{\Pi ,y}(a)=b$ .
По произвольной программе $\Pi$ определить, является ли множество значений вычисляемой ею функции $\Phi _{\Pi ,y}(x)$ бесконечным.
По произвольной паре программ $\Pi$ и $\Pi '$ проверить, что для всех x имеет место неравенство $\Phi _{\Pi ,y}(x) > \Phi _{\Pi ',y}(x)$ .