|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Проблема представления данных
Дробные p-адические числа.
ОПРЕДЕЛЕНИЕ. Дробь вида  ,
,  , k >= 0 определяет дробное p -адическое число или просто p -адическое число. Две
дроби,
, k >= 0 определяет дробное p -адическое число или просто p -адическое число. Две
дроби,  и
и  , определяют одно и тоже p -адическое число, если
, определяют одно и тоже p -адическое число, если  в
в  .
.
Совокупность всех p -адических чисел обозначается Rp. Легко проверить, что операции сложения и умножения продолжаются с Op на Rp и превращают Rp в поле.
2.9. ТЕОРЕМА. Всякое p -адическое число  единственным
образом представляется в виде
единственным
образом представляется в виде
 |
( 2.8) |
где m — целое число, а  — единица кольца Op.
— единица кольца Op.
2.10. ТЕОРЕМА. Всякое отличное от нуля p -адическое число  однозначно представляется в виде
однозначно представляется в виде
 |
( 2.9) |
где  .
.
Аксиоматическая характеристика поля p-адических чисел.
Выбрав некоторое вещественное число  такое, что
такое, что  , (например,
, (например,  ) положим
) положим
 |
( 2.10) |
ОПРЕДЕЛЕНИЕ. Функция  ,
,  , определенная
условиями (2.10), называется
, определенная
условиями (2.10), называется  - адической
метрикой . Значение
- адической
метрикой . Значение  называется
величиной
называется
величиной  - адического числа
- адического числа  в этой
метрике.
в этой
метрике.
Как и в случае показателя, функцию  иногда будем называть
просто метрикой и обозначать
иногда будем называть
просто метрикой и обозначать 
Легко проверяется, что p -адическая метрика обладает следующими свойствами:
 |
( 2.11) |
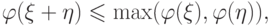 |
( 2.12) |
 |
( 2.13) |
Свойства (2.11) и (2.13) указывают, что введенное понятие является аналогом абсолютной величины в поле вещественных чисел.
2.12. ОПРЕДЕЛЕНИЕ. Пусть k — произвольное поле. Функция  определенная на элементах
определенная на элементах  поля k и принимающая вещественные
значения
поля k и принимающая вещественные
значения  , называется метрикой поля k, если она обладает
следующими свойствами:
, называется метрикой поля k, если она обладает
следующими свойствами:
-
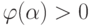 при
при  ;
;  ;
; -
 ;
; -
 .
.
Поле k вместе с заданной в нем метрикой  называется метризованным полем.
называется метризованным полем.
Из определения легко вытекают следующие свойства метрик:

Метриками являются:
- абсолютная величина в поле рациональных чисел;
- абсолютная величина в поле вещественных чисел;
- модуль в поле комплексных чисел;
-
 - адическая метрика
- адическая метрика  в поле
в поле  - адических чисел
- адических чисел  ;
; - функция
 , определенная в произвольном поле
, определенная в произвольном поле  условиями:
условиями:  ,
,  при
при  .
Такая метрика называется тривиальной.
.
Такая метрика называется тривиальной.
Если метрику  поля
поля  мы рассматриваем
лишь на рациональных числах, то получаем некоторую новую метрику поля
рациональных чисел
мы рассматриваем
лишь на рациональных числах, то получаем некоторую новую метрику поля
рациональных чисел  . Эта метрика, обозначаемая также через
. Эта метрика, обозначаемая также через  , называется
, называется  - адической метрикой поля
- адической метрикой поля  .
.
Аксиоматически поля вещественных и  -адических чисел
можно определить следующим образом.
-адических чисел
можно определить следующим образом.
Поле вещественных чисел  — это пополнение поля рациональных чисел
— это пополнение поля рациональных чисел  по метрике 1.
по метрике 1.
Поле  - адических чисел
- адических чисел  —
это пополнение поля рациональных чисел
—
это пополнение поля рациональных чисел  по
по  - адической метрике.
- адической метрике.
2.14. УПРАЖНЕНИЕ. Представить число -1 в поле p -адических чисел в виде ряда (2.9).
2.15. УПРАЖНЕНИЕ.
Представить число  в поле 5-адических чисел в виде ряда (2.9).
в поле 5-адических чисел в виде ряда (2.9).
2.16. УПРАЖНЕНИЕ. Доказать для многочленов над полем p -адических чисел признак неприводимости Эйзенштейна: многочлен f(x) = a0xn + a1xn-1 + · · · + an с целыми p -адическими коэффициентами неприводим над полем Rp, если a0 не делится на p, все остальные коэффициенты a1, . . . , an делятся на p и свободный член an, делясь на p, не делится на p2.
