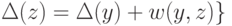|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Кратчайшие пути
Алгоритм Дейкстры
Допустим, на некотором шаге описанного выше алгоритма построено дерево
с множеством вершин  , а для каждой вершины
, а для каждой вершины  известна
вершина
известна
вершина  , на которой достигается наименьшее значение
величины
, на которой достигается наименьшее значение
величины  , где минимум берется
по всем вершинам
, где минимум берется
по всем вершинам  . Тогда на этом шаге следует выбрать
вершину
. Тогда на этом шаге следует выбрать
вершину  с наименьшим значением величины
с наименьшим значением величины  и присоединить к дереву ребро
и присоединить к дереву ребро  . После этого для каждой
вершины
. После этого для каждой
вершины 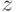 , еще не принадлежащей к дереву, значения
, еще не принадлежащей к дереву, значения  и
и  уточняются следующим образом: если
уточняются следующим образом: если  ,
то следует положить
,
то следует положить  ,
,  .
Вершина
.
Вершина  может рассматриваться как предполагаемый отец
вершины
может рассматриваться как предполагаемый отец
вершины  в геодезическом дереве (если все
множество
в геодезическом дереве (если все
множество 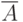 состояло бы из одной
вершины
состояло бы из одной
вершины  , то
, то  была бы ее истинным отцом).
Величина
была бы ее истинным отцом).
Величина 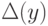 представляет собой оценку кратчайшего
пути из
представляет собой оценку кратчайшего
пути из  в
в  , она равна весу кратчайшего из путей,
проходящих только через вершины
множества
, она равна весу кратчайшего из путей,
проходящих только через вершины
множества  . После того, как вершина
. После того, как вершина  присоединяется
к дереву, значения
присоединяется
к дереву, значения  и
и 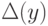 больше не
изменяются,
больше не
изменяются,  является отцом вершины
является отцом вершины  в геодезическом дереве,
а
в геодезическом дереве,
а  .
В целом алгоритм можно представить следующим образом:
.
В целом алгоритм можно представить следующим образом:
Алгоритм 2. Алгоритм Дейкстры.
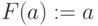

-
for
 do
do  ;
; 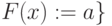
-
while
 do
do
- выбрать вершину
 с наименьшим
значением
с наименьшим
значением 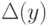

-
for
 do
do
-
if
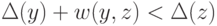
-
then
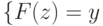 ,
,