|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Оптимальные каркасы
Оценим время работы алгоритма Прима. Цикл while в строке 4
повторяется один раз для каждой вершины графа, кроме стартовой. Внутри
этого цикла есть еще скрытый цикл в строке 5, где ищется ребро наименьшего
веса среди всех ребер, соединяющих вершины из множества  с вершинами, не принадлежащими
с вершинами, не принадлежащими  . Допустим, что этот поиск
производится самым бесхитростным образом, т.е. просматриваются все пары
вершин
. Допустим, что этот поиск
производится самым бесхитростным образом, т.е. просматриваются все пары
вершин  с
с  ,
,  .
Если
.
Если 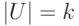 , то
имеется
, то
имеется  таких пар. Так как k меняется от 1
до
таких пар. Так как k меняется от 1
до  , то всего получаем
, то всего получаем
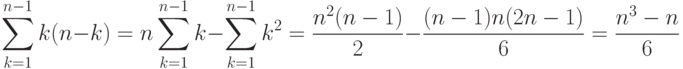
пар, которые нужно рассмотреть. Таким образом, трудоемкость алгоритма
будет  .
.
Небольшое усовершенствование позволяет на порядок ускорить этот алгоритм.
Допустим, что для каждой вершины  из множества
из множества  известна такая вершина
известна такая вершина  , что
, что  .
Тогда при
.
Тогда при 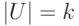 необходимо будет выбрать ребро наименьшего веса среди
необходимо будет выбрать ребро наименьшего веса среди  ребер,
а общее число анализируемых ребер будет равно
ребер,
а общее число анализируемых ребер будет равно
 |
( 1) |
В этом случае, однако, необходимы дополнительные действия для обновления
таблицы значений функции  при добавлении одной вершины к дереву,
т.е. при переносе одной вершины из множества
при добавлении одной вершины к дереву,
т.е. при переносе одной вершины из множества  в множество
в множество  . Сначала, когда множество
. Сначала, когда множество  состоит
из
единственной вершины
состоит
из
единственной вершины  , полагаем
, полагаем  для всех
для всех  . В дальнейшем эти значения могут меняться. Допустим,
на
некотором шаге к дереву присоединяется вершина
. В дальнейшем эти значения могут меняться. Допустим,
на
некотором шаге к дереву присоединяется вершина  . Тогда для
каждой
вершины
. Тогда для
каждой
вершины 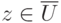 либо сохраняется старое значение
либо сохраняется старое значение  ,
либо устанавливается новое
,
либо устанавливается новое  , в зависимости от того, какое
из
ребер
, в зависимости от того, какое
из
ребер  и
и  имеет меньший вес. Иначе
говоря, для
модификации функции
имеет меньший вес. Иначе
говоря, для
модификации функции  достаточно в алгоритме 10 после строки 8
(и внутри цикла while ) добавить
следующее:
достаточно в алгоритме 10 после строки 8
(и внутри цикла while ) добавить
следующее:
-
for
 do
do
-
if
 then
then 
При 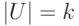 цикл в строке 9 повторяется
цикл в строке 9 повторяется  раз.
Таким
образом, дополнительное время, необходимое для обслуживания
таблицы
раз.
Таким
образом, дополнительное время, необходимое для обслуживания
таблицы  , тоже оценивается сверху квадратичной функцией
от
, тоже оценивается сверху квадратичной функцией
от  и общая оценка трудоемкости усовершенствованного алгоритма Прима
будет
и общая оценка трудоемкости усовершенствованного алгоритма Прима
будет  .
.
Другой путь к усовершенствованию алгоритма Прима подсказывает следующее
замечание. При выборе подходящего ребра (в строке 5 алгоритма 10) можно
рассматривать не все пары  , а только те,
которые являются ребрами графа. Если граф разреженный, т.е. содержит
намного меньше ребер, чем полный граф, то это может значительно ускорить
решение задачи. Дополнительный выигрыш можно получить, если использовать
приоритетную очередь для хранения множества ребер, подлежащих
исследованию.
, а только те,
которые являются ребрами графа. Если граф разреженный, т.е. содержит
намного меньше ребер, чем полный граф, то это может значительно ускорить
решение задачи. Дополнительный выигрыш можно получить, если использовать
приоритетную очередь для хранения множества ребер, подлежащих
исследованию.
