|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Важнейшие классы графов
Двудольные графы
Граф называется двудольным,
если множество его вершин можно так
разбить на два подмножества, чтобы концы каждого ребра принадлежали разным
подмножествам. Эти подмножества называются долями. Таким образом,
каждая из долей порождает пустой подграф. Примером двудольного графа
является простая цепь  при любом
при любом  : одна доля
порождается
вершинами с четными номерами, другая - с нечетными. Граф
: одна доля
порождается
вершинами с четными номерами, другая - с нечетными. Граф  -
пример графа, не являющегося двудольным: при любом разбиении множества его
вершин на два подмножества в одном из этих подмножеств окажутся две
смежных вершины.
-
пример графа, не являющегося двудольным: при любом разбиении множества его
вершин на два подмножества в одном из этих подмножеств окажутся две
смежных вершины.
Прикладное значение понятия двудольного графа связано с тем, что с помощью
таких графов моделируются отношения между объектами двух типов, а такие
отношения часто встречаются на практике (например, отношение
"продукт  используется в производстве изделия
используется в производстве изделия  " между исходными
продуктами
и готовыми изделиями, или "работник
" между исходными
продуктами
и готовыми изделиями, или "работник  владеет
профессией
владеет
профессией  " между работниками и профессиями).
В математике такие отношения тоже нередки, один из наиболее
распространенных их видов - отношения
инцидентности. Пусть
" между работниками и профессиями).
В математике такие отношения тоже нередки, один из наиболее
распространенных их видов - отношения
инцидентности. Пусть  - множество, а
- множество, а  - семейство его
подмножеств. Элемент
- семейство его
подмножеств. Элемент  и множество
и множество  инцидентны
друг другу, если
инцидентны
друг другу, если 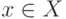 . Отношение инцидентности можно описать
с помощью двудольного графа
. Отношение инцидентности можно описать
с помощью двудольного графа  , в котором
, в котором  ,
,  . На рис. 3.3
показан граф отношения инцидентности для
. На рис. 3.3
показан граф отношения инцидентности для 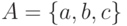 ,
, 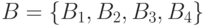 ,
где
,
где  ,
,  ,
,  ,
, 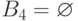 .
.
Вообще говоря, разбиение множества вершин двудольного графа на доли можно
осуществить не единственным способом. Так, в графе из только что
приведенного примера можно взять в качестве долей множества  и
и 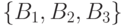 . В то же
время в самом
определении этого графа уже заложено "естественное" разбиение на
доли
. В то же
время в самом
определении этого графа уже заложено "естественное" разбиение на
доли  и
и  . Двудольные графы, возникающие в
приложениях, нередко бывают
заданы именно так - с множеством вершин, изначально состоящим из двух
частей, и с множеством ребер, каждое из которых соединяет вершины
из разных частей.
. Двудольные графы, возникающие в
приложениях, нередко бывают
заданы именно так - с множеством вершин, изначально состоящим из двух
частей, и с множеством ребер, каждое из которых соединяет вершины
из разных частей.
Если разбиение на доли не задано, то может возникнуть вопрос, существует
ли оно вообще, т.е. является ли данный граф двудольным? Если в
графе  вершин, то имеется
вершин, то имеется  разбиений множества вершин на два
подмножества и непосредственная проверка всех этих разбиений будет очень
трудоемким делом. Следующая теорема дает критерий двудольности, а из ее
доказательства можно извлечь и эффективный алгоритм проверки двудольности.
Подробно такой алгоритм будет описан в
"Поиск в ширину"
.
разбиений множества вершин на два
подмножества и непосредственная проверка всех этих разбиений будет очень
трудоемким делом. Следующая теорема дает критерий двудольности, а из ее
доказательства можно извлечь и эффективный алгоритм проверки двудольности.
Подробно такой алгоритм будет описан в
"Поиск в ширину"
.
Теорема 5. Следующие утверждения для графа  равносильны:
равносильны:
Доказательство.
Докажем, что из (1) следует (2). Пусть  -
двудольный граф, в котором выбрано некоторое разбиение на доли,
-
двудольный граф, в котором выбрано некоторое разбиение на доли,  - цикл длины
- цикл длины  в графе
в графе  .
При любом
.
При любом 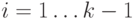 вершины
вершины  и
и  смежны
и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит
из всех вершин с нечетными индексами, т.е.
смежны
и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит
из всех вершин с нечетными индексами, т.е.  ,
другая - из всех вершин с четными индексами. Но
вершины
,
другая - из всех вершин с четными индексами. Но
вершины  и
и 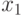 тоже смежны и должны принадлежать разным долям.
Следовательно,
тоже смежны и должны принадлежать разным долям.
Следовательно,  - четное число.
- четное число.
Очевидно, что из (2) следует (3); остается доказать, что из (3)
следует (1). Рассмотрим граф  , в котором нет простых
циклов нечетной длины. Ясно, что граф,
в котором каждая компонента связности - двудольный граф,
сам двудольный. Поэтому можно считать, что граф
, в котором нет простых
циклов нечетной длины. Ясно, что граф,
в котором каждая компонента связности - двудольный граф,
сам двудольный. Поэтому можно считать, что граф  связен.
Зафиксируем в нем некоторую вершину
связен.
Зафиксируем в нем некоторую вершину  и докажем, что для любых
двух
смежных между собой вершин
и докажем, что для любых
двух
смежных между собой вершин  и
и  имеет место
равенство
имеет место
равенство  . Действительно, допустим сначала, что
. Действительно, допустим сначала, что  . Пусть
. Пусть  -
кратчайший
путь из
-
кратчайший
путь из  в
в  -
кратчайший путь
из
-
кратчайший путь
из  в
в  . Эти пути начинаются в одной
вершине:
. Эти пути начинаются в одной
вершине:  ,
а оканчиваются в разных:
,
а оканчиваются в разных: 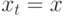 ,
, 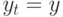 .
Поэтому найдется такое
.
Поэтому найдется такое  , что
, что  и
и  при всех
при всех  . Но тогда
последовательность
. Но тогда
последовательность  является простым циклом длины
является простым циклом длины  .
Следовательно,
.
Следовательно,  . Предположим,
что
. Предположим,
что  .
Если
.
Если  - кратчайший путь
из
- кратчайший путь
из  в
в  , то, очевидно, что
, то, очевидно, что  -
кратчайший путь из
-
кратчайший путь из  в
в  , следовательно,
, следовательно, 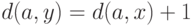 . Итак, расстояния от двух смежных вершин
до вершины
. Итак, расстояния от двух смежных вершин
до вершины  различаются ровно на единицу. Поэтому, если
обозначить
через
различаются ровно на единицу. Поэтому, если
обозначить
через  множество всех вершин графа, расстояние от которых
до вершины
множество всех вершин графа, расстояние от которых
до вершины  четно, а через
четно, а через  множество всех вершин
с нечетными
расстояниями до
множество всех вершин
с нечетными
расстояниями до  , то для каждого ребра графа один из его концов
принадлежит множеству
, то для каждого ребра графа один из его концов
принадлежит множеству  , другой -
множеству
, другой -
множеству  .
Следовательно, граф
.
Следовательно, граф  - двудольный.
- двудольный.
Пусть  - цикл в графе
- цикл в графе  . Множество вершин
цикла
. Множество вершин
цикла  порождает в
порождает в  подграф, который содержит все ребра этого цикла, но
может содержать и ребра, ему не принадлежащие. Такие ребра называют хордами цикла
подграф, который содержит все ребра этого цикла, но
может содержать и ребра, ему не принадлежащие. Такие ребра называют хордами цикла  .
Простой цикл, не имеющий хорд, - это порожденный
простой цикл. В графе, изображенном на рис. 3.4, хордами цикла
.
Простой цикл, не имеющий хорд, - это порожденный
простой цикл. В графе, изображенном на рис. 3.4, хордами цикла  являются ребра
являются ребра 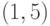 ,
, 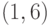 и
и  , а цикл
, а цикл 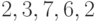 -
порожденный простой цикл. Заметим, что любой цикл длины
-
порожденный простой цикл. Заметим, что любой цикл длины  является
порожденным простым циклом.
является
порожденным простым циклом.
Пусть  - простой цикл длины
- простой цикл длины  в некотором
графе,
в некотором
графе,  - хорда этого цикла. Ребро
- хорда этого цикла. Ребро  вместе с ребрами цикла
вместе с ребрами цикла  образует два цикла меньшей длины,
образует два цикла меньшей длины, 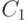 и
и 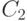 (см. рис. 3.5),
сумма длин которых равна
(см. рис. 3.5),
сумма длин которых равна  .
.
Значит, если  - цикл нечетной длины, то один из циклов
- цикл нечетной длины, то один из циклов 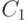 ,
, 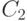 тоже имеет нечетную длину. Отсюда следует, что в графе,
в котором есть цикл нечетной длины, имеется и порожденный простой цикл
нечетной длины. Поэтому критерий двудольности справедлив и в следующей
формулировке.
тоже имеет нечетную длину. Отсюда следует, что в графе,
в котором есть цикл нечетной длины, имеется и порожденный простой цикл
нечетной длины. Поэтому критерий двудольности справедлив и в следующей
формулировке.
Следствие.Граф является двудольным тогда и только тогда, когда в нем нет порожденных простых циклов нечетной длины.



