|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Важнейшие классы графов
Центр дерева
Центр графа может состоять из одной вершины (как, например, в графе  ), а может включать все его вершины (полный граф). Для
дерева,
как мы увидим, имеется гораздо более узкий диапазон возможностей.
), а может включать все его вершины (полный граф). Для
дерева,
как мы увидим, имеется гораздо более узкий диапазон возможностей.
Теорема 3. Центр дерева состоит из одной вершины или из двух смежных вершин.
Доказательство.
Допустим, что в некотором дереве имеются две
несмежные центральные вершины 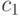 и
и 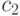 . На
пути,
соединяющем эти вершины, найдем промежуточную вершину
. На
пути,
соединяющем эти вершины, найдем промежуточную вершину  с
максимальным
эксцентриситетом, и пусть
с
максимальным
эксцентриситетом, и пусть 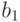 и
и  -
вершины, соседние
с
-
вершины, соседние
с  на этом пути (см. рис. 3.1).
Пусть
на этом пути (см. рис. 3.1).
Пусть  - вершина, наиболее удаленная
от
- вершина, наиболее удаленная
от  в дереве, т.е.
в дереве, т.е.  . Путь,
соединяющий
. Путь,
соединяющий  с
с  ,
не может проходить через обе вершины
,
не может проходить через обе вершины 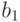 и
и  . Допустим,
он не проходит через
. Допустим,
он не проходит через 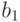 . Тогда единственный путь из
. Тогда единственный путь из 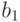 в
в  проходит через
проходит через  и
и 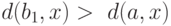 . Отсюда следует, что
. Отсюда следует, что  , а это противоречит выбору вершины
, а это противоречит выбору вершины  , если
, если 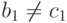 , или тому, что
, или тому, что 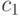 -
центральная вершина, если
-
центральная вершина, если  .
.
Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
Корневые деревья
Часто в дереве особо выделяется одна вершина, играющая роль своего рода
"начала отсчета". Дерево с выделенной вершиной называют корневым
деревом, а саму эту вершину - корнем. Из дерева с  вершинами
можно, таким образом, образовать
вершинами
можно, таким образом, образовать  различных корневых
деревьев.
различных корневых
деревьев.
При графическом изображении корневого дерева обычно придерживаются какого-нибудь стандарта. Один из наиболее распространенных состоит в следующем. Возьмем на плоскости семейство параллельных прямых с равными расстояниями между соседними прямыми. Изобразим корень точкой на одной из этих прямых, смежные с корнем вершины - точками на соседней прямой, вершины, находящиеся на расстоянии 2 от корня, - на следующей, и т.д. Ребра изобразим отрезками прямых. Ясно, что вершины на каждой прямой можно разместить так, чтобы ребра не пересекались. Пример нарисованного таким образом корневого дерева показан на рис. 3.2 (корень обведен кружком). Чаще, впрочем, дерево рисуют корнем вверх, а не вниз.
Иногда бывает полезно ребра корневого дерева ориентировать так, чтобы
в каждую вершину вел ориентированный путь из корня (для дерева
на рис. 3.2 это означает, что
каждое ребро
ориентируется снизу вверх). Такое
ориентированное корневое дерево будем называть исходящим деревом.
В исходящем дереве каждая вершина, кроме корня, является концом
единственного ребра. Если в исходящем дереве имеется ребро 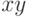 ,
то вершину
,
то вершину  называют отцом вершины
называют отцом вершины  , а вершину
, а вершину  - сыном
вершины
- сыном
вершины  . Естественный и для многих
целей удобный способ задания корневого дерева состоит в указании для
каждой вершины ее отца. При этом иногда считают, что корень приходится
отцом самому себе - это равносильно добавлению петли при корне.
. Естественный и для многих
целей удобный способ задания корневого дерева состоит в указании для
каждой вершины ее отца. При этом иногда считают, что корень приходится
отцом самому себе - это равносильно добавлению петли при корне.
Если в исходящем дереве  имеется ориентированный путь из
вершины
имеется ориентированный путь из
вершины  в вершину
в вершину  , то говорят, что
, то говорят, что  - предок
- предок  ,
а
,
а  - потомок
- потомок  . В частности, каждая вершина
является предком и потомком самой себя. Множество всех предков
вершины
. В частности, каждая вершина
является предком и потомком самой себя. Множество всех предков
вершины  порождает ориентированный путь из корня
в
порождает ориентированный путь из корня
в  . Множество всех
потомков вершины
. Множество всех
потомков вершины  порождает исходящее дерево с корнем
в
порождает исходящее дерево с корнем
в  ,
оно называется ветвью
дерева
,
оно называется ветвью
дерева  в вершине
в вершине  .
.
Высотой корневого дерева называется эксцентриситет его корня. Если мы хотим превратить некоторое дерево в корневое и притом минимальной высоты, то в качестве корня следует взять центральную вершину.
Каркасы
Пусть  - обыкновенный граф. Его каркасом называется
остовный подграф, в котором нет циклов, а области связности совпадают
с областями связности графа
- обыкновенный граф. Его каркасом называется
остовный подграф, в котором нет циклов, а области связности совпадают
с областями связности графа  . Таким образом, каркас связного
графа -
дерево, а в общем случае - лес.
. Таким образом, каркас связного
графа -
дерево, а в общем случае - лес.
У любого графа есть хотя бы один каркас. Действительно, если
в  нет циклов, то он сам является собственным каркасом. Если же циклы есть,
то можно удалить из графа любое ребро, принадлежащее какому-нибудь циклу.
Такое ребро не является перешейком, поэтому при его удалении области
связности не изменятся. Продолжая действовать таким образом, после
удаления некоторого количества ребер получим остовный подграф, в котором
циклов уже нет, а области связности - те же, что у исходного графа, то
есть этот подграф и будет каркасом. Можно даже точно сказать, сколько
ребер необходимо удалить для получения каркаса. Если в графе
нет циклов, то он сам является собственным каркасом. Если же циклы есть,
то можно удалить из графа любое ребро, принадлежащее какому-нибудь циклу.
Такое ребро не является перешейком, поэтому при его удалении области
связности не изменятся. Продолжая действовать таким образом, после
удаления некоторого количества ребер получим остовный подграф, в котором
циклов уже нет, а области связности - те же, что у исходного графа, то
есть этот подграф и будет каркасом. Можно даже точно сказать, сколько
ребер необходимо удалить для получения каркаса. Если в графе  вершин,
вершин,  ребер и
ребер и  компонент связности, то в
каркасе будет
тоже
компонент связности, то в
каркасе будет
тоже  вершин и
вершин и  компонент связности. Но в любом
лесе с
компонент связности. Но в любом
лесе с  вершинами и
вершинами и  компонентами связности имеется
ровно
компонентами связности имеется
ровно  ребер.
Значит, удалено будет
ребер.
Значит, удалено будет  ребер. Это число называется цикломатическим
числом графа и обозначается через
ребер. Это число называется цикломатическим
числом графа и обозначается через  .
.
Если в графе есть циклы, то у него больше одного каркаса. Определить
точное число каркасов связного графа позволяет так называемая матричная
теорема Кирхгофа. Приведем ее без доказательства. Для графа  определим матрицу
определим матрицу  - квадратную матрицу порядка
- квадратную матрицу порядка  с элементами
с элементами
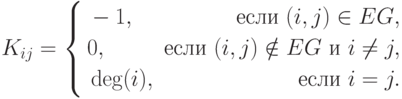
Иначе говоря,  получается из матрицы смежности, если
заменить
все
получается из матрицы смежности, если
заменить
все  на
на 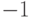 , а вместо нулей на главной диагонали
поставить степени вершин.
Заметим, что матрица
, а вместо нулей на главной диагонали
поставить степени вершин.
Заметим, что матрица  - вырожденная, так как сумма
элементов
каждой строки равна
- вырожденная, так как сумма
элементов
каждой строки равна  , то есть столбцы линейно зависимы.
, то есть столбцы линейно зависимы.


