|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Начальные понятия теории графов
Графы и бинарные отношения
Напомним, что бинарным
отношением на множестве  называется
любое подмножество
называется
любое подмножество  множества
множества  , состоящего из
всевозможных упорядоченных пар элементов множества
, состоящего из
всевозможных упорядоченных пар элементов множества  . Каждому
такому
отношению можно поставить в соответствие граф отношения
. Каждому
такому
отношению можно поставить в соответствие граф отношения  .
Сравнивая с тем, что говорилось выше об определениях различных типов
графов, видим, что понятие бинарного отношения эквивалентно понятию
ориентированного графа с петлями. Другие типы графов без кратных ребер -
это частные виды бинарных отношений. Отношение
.
Сравнивая с тем, что говорилось выше об определениях различных типов
графов, видим, что понятие бинарного отношения эквивалентно понятию
ориентированного графа с петлями. Другие типы графов без кратных ребер -
это частные виды бинарных отношений. Отношение  называется рефлексивным, если для
любого
называется рефлексивным, если для
любого  пара
пара  принадлежит
принадлежит  , и антирефлексивным,
если ни одна такая пара не
принадлежит
, и антирефлексивным,
если ни одна такая пара не
принадлежит  . Отношение называется симметричным, если из
. Отношение называется симметричным, если из 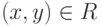 следует, что
следует, что  . В графе
антирефлексивного и симметричного отношения нет петель и для каждой пары
вершин либо нет ни одного, либо есть два ребра, соединяющих эти вершины.
Если в таком графе каждую пару ориентированных ребер, соединяющих одни
и те же две вершины, заменить одним неориентированным ребром, то получится
обыкновенный граф.
. В графе
антирефлексивного и симметричного отношения нет петель и для каждой пары
вершин либо нет ни одного, либо есть два ребра, соединяющих эти вершины.
Если в таком графе каждую пару ориентированных ребер, соединяющих одни
и те же две вершины, заменить одним неориентированным ребром, то получится
обыкновенный граф.
Откуда берутся графы
Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы - в этих случаях графы возникают естественно и видны "невооруженным глазом". При желании графы можно обнаружить практически где угодно. Это наглядно показано в книге Д.Кнута [D.E.Knuth, "The Stanford GraphBase"] - графы извлекаются из романа "Анна Каренина", из картины Леонардо да Винчи, из материалов Бюро Экономического Анализа США и из других источников.
Немало поводов для появления графов и в самой математике. Наиболее очевидный пример - любой многогранник в трехмерном пространстве. Вершины и ребра многогранника можно рассматривать как вершины и ребра графа. При этом мы отвлекаемся от того, как расположены элементы многогранника в пространстве, оставляя лишь информацию о том, какие вершины соединены ребрами. На рис. 1.4 показаны три способа изобразить один и тот же граф трехмерного куба.
Еще один способ образования графов из геометрических объектов иллюстрирует
рис. 1.5. Слева показаны шесть кругов
на плоскости,
а справа - граф, в котором каждая вершина соответствует
одному из этих кругов и две вершины
соединены ребром в том и только том случае, когда соответствующие круги
пересекаются. Такие графы называют графами пересечений. Можно построить
граф пересечений семейства интервалов на прямой, или дуг окружности, или
параллелепипедов. Вообще, для любого семейства
множеств 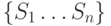 можно построить граф
пересечений с множеством вершин
можно построить граф
пересечений с множеством вершин  , в котором ребро
, в котором ребро 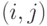 имеется тогда и
только
тогда, когда
имеется тогда и
только
тогда, когда  и
и 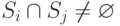 . Известно, что любой граф можно представить как граф пересечений
некоторого семейства множеств.
. Известно, что любой граф можно представить как граф пересечений
некоторого семейства множеств.
Число графов
Возьмем какое-нибудь множество 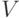 , состоящее из
, состоящее из  элементов,
и будем рассматривать всевозможные (обыкновенные!) графы с множеством
вершин
элементов,
и будем рассматривать всевозможные (обыкновенные!) графы с множеством
вершин 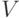 . Обозначим число таких графов через
. Обозначим число таких графов через  .
Эти графы
различаются только множествами ребер, а каждое ребро - это
неупорядоченная
пара различных элементов из
.
Эти графы
различаются только множествами ребер, а каждое ребро - это
неупорядоченная
пара различных элементов из 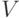 . В комбинаторике такие пары
называются
сочетаниями из
. В комбинаторике такие пары
называются
сочетаниями из  по 2, их число равно
по 2, их число равно
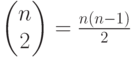
Теорема 1.  .
.
Смежность, инцидентность, степени
Если в графе имеется ребро 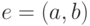 , то говорят, что вершины
, то говорят, что вершины  и
и  смежны в этом графе, ребро
смежны в этом графе, ребро  инцидентно
каждой из вершин
инцидентно
каждой из вершин  ,
,  , а каждая из них инцидентна
этому ребру.
, а каждая из них инцидентна
этому ребру.
Множество всех вершин графа, смежных с данной вершиной  ,
называется окрестностью этой вершины и
обозначается
через
,
называется окрестностью этой вершины и
обозначается
через 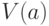 .
.
На практике удобным и эффективным при решении многих задач способом
задания графа являются так называемые списки смежности. Эти списки могут
быть реализованы различными способами в виде конкретных структур данных,
но в любом случае речь идет о том, что для каждой вершины  перечисляются все смежные с ней вершины, т.е. элементы множества
перечисляются все смежные с ней вершины, т.е. элементы множества 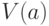 . Такой способ задания дает возможность быстрого
просмотра окрестности вершины.
. Такой способ задания дает возможность быстрого
просмотра окрестности вершины.
Число вершин, смежных с вершиной  , называется степенью
вершины
, называется степенью
вершины  и обозначается через
и обозначается через  .
.
Если сложить степени всех вершин некоторого графа, то каждое ребро внесет в эту сумму вклад, равный 2, поэтому справедливо следующее утверждение:
Теорема 2. 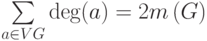 .
.
Это равенство известно как "лемма о рукопожатиях". Из него следует, что число вершин нечетной степени в любом графе четно.
Вершину степени  называют изолированной.
называют изолированной.
Граф называют регулярным
степени 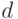 , если степень каждой его
вершины равна
, если степень каждой его
вершины равна 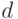 .
.
Набор степеней графа - это последовательность степеней его вершин, выписанных в неубывающем порядке.


