|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Разделенные множества
Представление разделенных множеств с использованием рангов вершин
Предыдущую реализацию разделенных множеств можно усовершенствовать следующим образом. Операцию ОБЪЕДИНИТЬ можно выполнить так, чтобы высота дерева, соответствующего объединению двух множеств, была как можно меньше. А именно, корень большего по высоте дерева сделать родителем корня другого дерева. Назовем такую реализацию операции ОБЪЕДИНИТЬ объединением по рангу. В качестве ранга в данном случае берется высота соответствующего дерева.
Реализация операций с использованием рангов вершин
Для такой реализации разделенных множеств необходимо хранить с каждым
узлом  дополнительно еще одну величину — высоту поддерева,
корнем которого является узел
дополнительно еще одну величину — высоту поддерева,
корнем которого является узел  . Будем называть ее высотой, или рангом,
узла
. Будем называть ее высотой, или рангом,
узла  . Остальные операции нужно настроить на корректную работу с
этим полем. Будем хранить высоту каждого узла
. Остальные операции нужно настроить на корректную работу с
этим полем. Будем хранить высоту каждого узла  в
ячейке
в
ячейке ![h[x]](/sites/default/files/tex_cache/bd57f1a9c1d9bd021644e22ab29e5e77.png) массива
массива 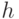 .
.
Операция СОЗДАТЬ (  ) назначает в качестве родителя
узла
) назначает в качестве родителя
узла  тот
же самый
тот
же самый  , а высотой узла
, а высотой узла  считает 0. Таким образом,
время выполнения данной операции есть
считает 0. Таким образом,
время выполнения данной операции есть  . В результате выполнения
операции СОЗДАТЬ (
. В результате выполнения
операции СОЗДАТЬ (  ) образуется новое дерево, изображенное
на рис. 3.6.
Число, расположенное рядом с узлом, обозначает его высоту. Описанные
действия реализуются с помощью операторов
) образуется новое дерево, изображенное
на рис. 3.6.
Число, расположенное рядом с узлом, обозначает его высоту. Описанные
действия реализуются с помощью операторов
![\formula{
p[x]:= x;\ h[x]:= 0;
}](/sites/default/files/tex_cache/1667aa6e94d65f7dfd2710ac81d6aace.png)
Операция ОБЪЕДИНИТЬ
(  ) назначает корень большего
по высоте дерева родителем корня другого дерева. Если деревья имеют
одинаковую высоту, то узел
) назначает корень большего
по высоте дерева родителем корня другого дерева. Если деревья имеют
одинаковую высоту, то узел  назначается родителем
узла
назначается родителем
узла  ,
после чего значение высоты узла
,
после чего значение высоты узла  увеличивается на единицу.
Заметим, что
увеличивается на единицу.
Заметим, что  и
и  должны быть до выполнения операции корнями
соответствующих деревьев. Именем вновь образованного подмножества будет
имя того из объединяемых подмножеств, у которого корень имел большую
высоту, а имя другого из объединяемых подмножеств перестанет быть именем
какого-либо из подмножеств. Очевидно, время выполнения этой операции есть
константа. Выполнить описанные действия можно с помощью следующей
процедуры:
должны быть до выполнения операции корнями
соответствующих деревьев. Именем вновь образованного подмножества будет
имя того из объединяемых подмножеств, у которого корень имел большую
высоту, а имя другого из объединяемых подмножеств перестанет быть именем
какого-либо из подмножеств. Очевидно, время выполнения этой операции есть
константа. Выполнить описанные действия можно с помощью следующей
процедуры:
![\formula{
\t{Procedure ОБЪЕДИНИТЬ (x,
y)};\\
\t begin\\
\mbox{}\q if (h[x] < h[y])\
\t then\
p[x] := y\ \t else if\ (h[x] >
h[y])\ \t then\
p[y] := x\ \t else\\
\mbox{}\qq
\{p[x] := y;\ h[y] := h[y] + 1\}\\
\t end;
}](/sites/default/files/tex_cache/1336ee41e1d3bba45fe91cb76f96dcf1.png)
На рис. 3.7 и рис. 3.8 показано применение
операции ОБЪЕДИНИТЬ 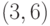 к коллекции,
изображенной на рис. 3.3, с учетом высот объединяемых поддеревьев. Рядом
с кружочками, изображающими узлы, показаны их высоты.
Так как
к коллекции,
изображенной на рис. 3.3, с учетом высот объединяемых поддеревьев. Рядом
с кружочками, изображающими узлы, показаны их высоты.
Так как  , то родителем узла 6 становится
узел 3.
, то родителем узла 6 становится
узел 3.
Операция НАЙТИ (  ) осуществляется, как
и в предыдущей реализации, продвижением по указателям на родителей
от узла
) осуществляется, как
и в предыдущей реализации, продвижением по указателям на родителей
от узла  до корня дерева. В качестве
до корня дерева. В качестве  берется
найденный корень.
берется
найденный корень.
Очевидно, что время выполнения данной операции, как и ранее,
пропорционально длине пути из узла  в корень соответствующего
дерева. Однако длина такого пути в данном случае может быть оценена иначе.
Для оценки длины этого пути докажем следующие леммы:
в корень соответствующего
дерева. Однако длина такого пути в данном случае может быть оценена иначе.
Для оценки длины этого пути докажем следующие леммы:
Лемма 1.
В результате выполнения любой последовательности операций
из набора 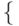 СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ
СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ  над пустой
коллекцией разделенных
множеств для любого узла
над пустой
коллекцией разделенных
множеств для любого узла  выполняется неравенство
выполняется неравенство ![n[x]\ge
2^{h(x)}](/sites/default/files/tex_cache/d6a27f24492d668e50347507cc29d219.png) ,
где
,
где ![n[x]](/sites/default/files/tex_cache/0545ee1aa896d0a11b6ade6084ac9e72.png) — количество узлов в поддереве
с корнем
— количество узлов в поддереве
с корнем ![x, h[x]](/sites/default/files/tex_cache/8e6444999c48476064a62ff68860371a.png) — высота узла
— высота узла  .
.
Доказательство
Очевидно, перед первым применением операции
ОБЪЕДИНИТЬ для любого узла  имели
имели ![n[x] =
1](/sites/default/files/tex_cache/966b1d9a19407f9fe89609750647f405.png) ,
, ![h[x] = 0](/sites/default/files/tex_cache/e1112fe3df4a14b1241cb1cfa4137bca.png) и, следовательно,
и, следовательно, ![n[x] \ge 2^{h(x)}](/sites/default/files/tex_cache/e3ff36d0b5733b8e447e717ea3089a46.png) .
Операции СОЗДАТЬ и НАЙТИ не могут нарушить доказываемого неравенства,
поэтому доказательство можно провести индукцией по количеству применений
операции ОБЪЕДИНИТЬ.
.
Операции СОЗДАТЬ и НАЙТИ не могут нарушить доказываемого неравенства,
поэтому доказательство можно провести индукцией по количеству применений
операции ОБЪЕДИНИТЬ.
Предположим, что перед очередным применением операции ОБЪЕДИНИТЬ
(  ) доказываемое неравенство все еще остается верным, тогда если
высота узла
) доказываемое неравенство все еще остается верным, тогда если
высота узла  меньше высоты узла
меньше высоты узла  , то дерево,
полученное с помощью ОБЪЕДИНИТЬ (
, то дерево,
полученное с помощью ОБЪЕДИНИТЬ (  ), имеет корень
), имеет корень  , а высоты
узлов
, а высоты
узлов  и
и  не изменились. Количество узлов в дереве
с корнем
не изменились. Количество узлов в дереве
с корнем  не изменилось, а количество узлов в дереве с
корнем
не изменилось, а количество узлов в дереве с
корнем  увеличилось. Таким образом, как для
узлов
увеличилось. Таким образом, как для
узлов  ,
,  , так и для всех
остальных неравенство сохраняется. Случай, когда высота
узла
, так и для всех
остальных неравенство сохраняется. Случай, когда высота
узла  больше высоты узла
больше высоты узла  , аналогичен
рассмотренному.
, аналогичен
рассмотренному.
Если же высоты деревьев с корнями  и
и  до
выполнения операции были одинаковы (
до
выполнения операции были одинаковы ( ![h[x] = h[y] = h)](/sites/default/files/tex_cache/3d5ad2a98756a4a3f042447c51c8519e.png) , то
узел
, то
узел  становится родителем
узла
становится родителем
узла  , высота узла
, высота узла  увеличивается на 1, а высота
узла
увеличивается на 1, а высота
узла  не изменяется. Пусть после
выполнения операции
величины
не изменяется. Пусть после
выполнения операции
величины ![h[x]](/sites/default/files/tex_cache/bd57f1a9c1d9bd021644e22ab29e5e77.png) ,
, ![h[y]](/sites/default/files/tex_cache/f7138c90084e712310529dd364afca7c.png) ,
, ![n[x]](/sites/default/files/tex_cache/0545ee1aa896d0a11b6ade6084ac9e72.png) ,
, ![n[y]](/sites/default/files/tex_cache/e317e0cd71772b2e3aa8b17647c4361b.png) становятся
равными соответственно
становятся
равными соответственно ![h'[x]](/sites/default/files/tex_cache/749fb5967085c792306fa004745295d7.png) ,
, ![h'[y]](/sites/default/files/tex_cache/3a9d559bbab551a80ed373d6063d7f70.png) ,
, ![n'[x]](/sites/default/files/tex_cache/af6efb88ad7eb945a4d6ed3e7fe8f3fc.png) ,
, ![n'[y]](/sites/default/files/tex_cache/f98e08f1dcf7dc674b50a4f2190969b5.png) ,
тогда имеем
,
тогда имеем ![h'[y] = h [y] + 1](/sites/default/files/tex_cache/b9e4e0991331c061bbea12e30060d901.png) ,
, ![h'[x] =
h[x]](/sites/default/files/tex_cache/bb098a268a0bdb111f2237c04c57cf76.png) ,
, ![n'[x] = n[x]](/sites/default/files/tex_cache/a98c0d1df1ab9d1e4e681d0c017eae81.png) ,
, ![n'[y] = n[y] + n[x]](/sites/default/files/tex_cache/6dbfc5e7774e4111e509a295f83cacca.png) . По
предположению индукции, имеем
. По
предположению индукции, имеем ![n[y] \ge 2^{h[y]}](/sites/default/files/tex_cache/6aac7e9b004818501a0e44102d8a843a.png) и
и ![n[x] \ge 2^{h[x]}](/sites/default/files/tex_cache/78cd7bc829d95b867ebab1155352210f.png) .
Следовательно, после выполнения рассматриваемой
операции для узлов
.
Следовательно, после выполнения рассматриваемой
операции для узлов  и
и  имеем соотношения
имеем соотношения
![\eqa*{
n'[x] & = n[x] \ge 2^{h[x]} = 2^{h' [x]}\q \t{и }\\
n'[y] & = n[y] + n[x] \ge 2^{h [y]} + 2^{h [x]} = 2^{h + 1} = 2^{h' [y]}.
}](/sites/default/files/tex_cache/4d4592abaab93209ee72644cd10c01ad.png)
Лемма 2.
Если за время работы, начавшейся с пустой коллекции,
операция СОЗДАТЬ применялась  раз, то для любого
раз, то для любого  число
число  узлов высоты
узлов высоты 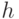 удовлетворяет
неравенству
удовлетворяет
неравенству  .
.
Доказательство
Пусть  — все
узлы высоты
— все
узлы высоты 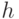 , тогда по лемме 1 при
, тогда по лемме 1 при  справедливы неравенства
справедливы неравенства ![{n[x_i] \!\ge\! 2^h}](/sites/default/files/tex_cache/9b531ae6fbb4d99f418f82cd026211e1.png) . Таким образом,
. Таким образом,
![\eq*{
n \ge n[x_1] + n[x_2] + ... + n[x_k] \ge k2^h,
}](/sites/default/files/tex_cache/202274b81e52606aea5d83fe4c35c836.png)
 .
.Следствие 3.
В результате выполнения любой последовательности
операций из набора 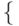 СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ
СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ 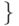 над
пустой коллекцией разделенных множеств для любого узла
над
пустой коллекцией разделенных множеств для любого узла  имеет место
неравенство
имеет место
неравенство ![h[x] \le \log n](/sites/default/files/tex_cache/509a152578ea7329289943f92a086364.png) .
.
Доказательство
Дерево максимальной высоты образуется, очевидно,
лишь тогда, когда все  элементов объединяются в одно множество.
Для такого дерева количество
элементов объединяются в одно множество.
Для такого дерева количество  узлов максимальной
высоты
узлов максимальной
высоты 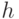 равно 1,
по лемме 2 имеем
равно 1,
по лемме 2 имеем  , откуда
, откуда  и,
следовательно,
и,
следовательно,  .
.
Следствие 4.
Время выполнения операции НАЙТИ есть  .
.
Следствие 5.
При реализации разделенных множеств с использованием
рангов время выполнения  операций ОБЪЕДИНИТЬ и
операций ОБЪЕДИНИТЬ и  или
НАЙТИ есть величина
или
НАЙТИ есть величина  .
.
Замечание При реализации операции объединения подмножеств в качестве ранга узла можно использовать количество узлов в поддереве с корнем в данном узле. Утверждение леммы 1 будет справедливым и в этом случае, следовательно, сохранятся и оценки времени выполнения операций.



